Active vs. Passive Harmonic Filters: Key Differences
Advertisement
Harmonic filters are crucial for reducing harmonic distortion in electrical systems. They help ensure power quality and protect sensitive equipment from the damaging effects of harmonic currents. Harmonics are voltage or current waveforms with frequencies that are integer multiples of the fundamental frequency (e.g., 50 Hz or 60 Hz).
There are two primary types of harmonic filters: Active Harmonic Filters (AHF) and Passive Harmonic Filters (PHF). Let’s dive into the differences, advantages, and disadvantages of each.
Active Harmonic Filter
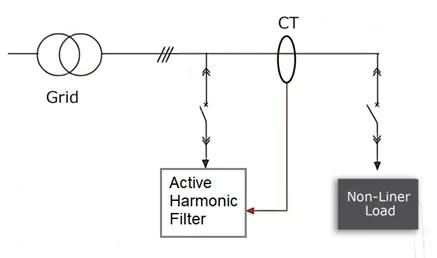
Active Harmonic Filters are electronic devices designed to dynamically cancel harmonic currents. They achieve this by injecting currents that are equal in magnitude but opposite in phase to the harmonics present in the system, effectively reducing or eliminating harmonics in real-time.
AHFs typically utilize power electronics, microprocessors, and fast-switching IGBTs (Insulated Gate Bipolar Transistors) to generate compensating signals. They are commonly used in industrial environments, commercial buildings, and facilities with variable speed drives, uninterruptible power supplies (UPS), or other nonlinear loads that generate significant harmonic levels.
How Active Harmonic Filters Work
An active harmonic filter continuously monitors the electrical system for harmonics. Once detected, it generates a compensating signal (anti-harmonic currents) and injects it into the system. This effectively cancels out the unwanted harmonic currents, improving overall power quality.
Advantages of Active Harmonic Filters
- Real-time response: Adapts to changing harmonic conditions dynamically.
- Wide range compensation: Can compensate for a broad spectrum of harmonic orders.
- Dynamic power factor correction: Provides power factor correction and handles unbalanced loads.
- High-order harmonic correction: Capable of correcting higher-order harmonics, even up to the 50th order and beyond.
Disadvantages of Active Harmonic Filters
- Higher initial cost: Due to the complex electronic components involved.
- External power source required: Needs an external power source for operation.
- Maintenance: Requires regular maintenance and skilled personnel for operation and troubleshooting.
Passive Harmonic Filter
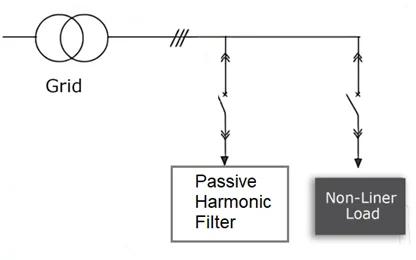
Passive Harmonic Filters utilize passive components such as inductors (L), capacitors (C), and resistors (R) to attenuate or block specific harmonic frequencies from entering the system. They are typically tuned to a specific harmonic frequency (e.g., 5th, 7th harmonic) and are designed for steady-state harmonic mitigation.
These filters are arranged in various configurations, such as series, parallel, or a combination of both. Passive filters are generally used in systems with relatively stable harmonic content, such as motor drives, fixed-frequency power supplies, or industrial machinery.
How Passive Harmonic Filters Work
Passive filters are tuned circuits that resonate at specific harmonic frequencies. When these harmonics pass through the filter, they are either absorbed or diverted to ground, preventing them from flowing back into the power network.
Advantages of Passive Harmonic Filters
- Simple design: Easier to implement compared to active filters.
- No external power source required: Operates without the need for an external power supply.
- Lower cost: Typically less expensive than active filters.
- Reliable and rugged: Requires minimal maintenance.
Disadvantages of Passive Harmonic Filters
- Less effective at reducing higher-order harmonics.
- Static performance: Not suitable for dynamically changing harmonic conditions.
- Potential resonance issues: If not correctly designed or applied, resonance problems can occur.
- Limited frequency reduction: Restricted to reducing harmonics for specific frequencies only.
Difference Between Active and Passive Harmonic Filters
The following table highlights the key differences between active and passive harmonic filters:
| Parameter | Active Harmonic Filter | Passive Harmonic Filter |
|---|---|---|
| Technology | Uses power electronics and microprocessors. | Uses passive components like inductors, capacitors, and resistors. |
| Response Time | Real-time dynamic response to changing conditions. | Fixed response based on tuned harmonic frequency. |
| Harmonic Orders | Compensates for a wide range of harmonic orders. | Typically tuned to specific harmonic orders. |
| Effectiveness | Highly effective at reducing both low- and high-order harmonics. | Limited effectiveness; better at lower-order harmonics. |
| Power Factor Correction | Provides dynamic power factor correction. | Limited power factor correction capability. |
| Voltage/Current Balancing | Can balance voltage and current in three-phase systems. | No voltage or current balancing capability. |
| Maintenance | Requires regular maintenance and skilled personnel. | Low maintenance and easy to handle. |
| External Power Source | Needs an external power source for operation. | No external power source needed. |
| Flexibility | Flexible, can be used for different load conditions. | Fixed design, less flexible for changing conditions. |
| Size and Weight | Larger and heavier due to power electronics. | Generally smaller and lighter. |
| Cost | Higher initial and operating costs. | Lower initial cost with minimal operating expenses. |
| Application Suitability | Variable/high harmonic content environments. | Stable harmonic conditions environments. |
Conclusion
Both active and passive harmonic filters effectively reduce harmonic distortion in electrical systems, but they differ in their functionality and application. Active filters provide dynamic and precise harmonic mitigation with better control over variable loads, making them ideal for complex industrial setups. Passive filters are simpler, more cost-effective, and suitable for applications with stable, predictable harmonic profiles. The choice between them depends on the complexity of the load, budget, and desired level of harmonic reduction. Hybrid solutions that combine both technologies can also be considered for achieving optimal harmonic mitigation and power quality.
Advertisement
 RF
RF