All Pass Filter (APF) Basics: Design and Applications

This page covers the basics of All Pass Filters (APF), comparing first and second order designs. Usually, the amplitude response is key in filtering. Based on this, filters are named LPF (Low Pass Filter), HPF (High Pass Filter), and so on.

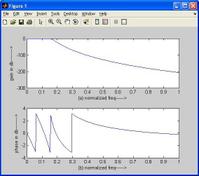
An All Pass Filter, however, doesn’t change the amplitude of the input signal. Instead, it introduces a phase shift. It’s also known as an ‘APF’ filter. The main function of an All Pass Filter is to introduce a phase shift or phase delay.

• The amplitude of the filter remains unity (1) for all frequencies.
• The phase response changes from 0 degrees to 360 degrees.

All Pass Filter Applications

• Phase Equalization: APFs are used to correct phase distortion.
• SSB-SC Modulation: Used in Single Side Band Suppressed Carrier modulation circuit designs.

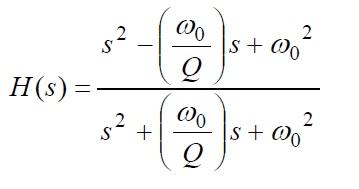
All Pass Filter Transfer Function

The Transfer function of an All Pass Filter can be expressed as:

H_AP = H_LP - H_BP + H_HP = 1 - 2 * H_BP

First Order vs Second Order All Pass Filter

All-Pass Filters are typically built using Operational Amplifiers along with discrete resistors and capacitors. Let’s look at the first and second order circuit designs.

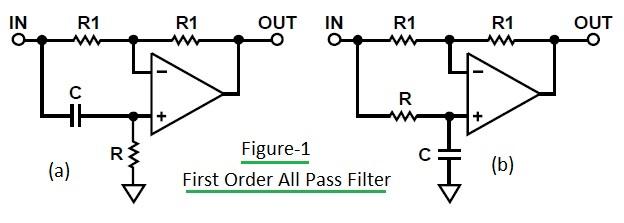
First Order All-Pass Filter

Figure 1 shows a First Order All Pass Filter circuit. Fig-1 (a) depicts the high pass equivalent, and fig-1 (b) the low pass equivalent. The circuit in fig-1(a) has a phase shift variation from -180 degrees (at 0 Hz) to 0 degrees (at higher frequencies). At w = 1/RC, the phase shift is -90 degrees. A variable resistor can be used to adjust the delay at a specific frequency.

The circuit in fig-1(b) has a phase shift variation from 0 degrees (at DC) to -180 degrees (at higher frequencies).

First Order APF Design Equations

The equations above are used for the high pass equivalent first order all pass filter design (as shown in fig-1 (a)).

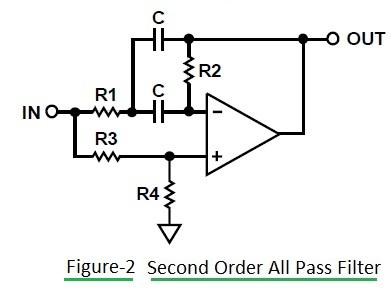
Second Order All-Pass Filter

Figure 2 depicts a Second Order All Pass Filter circuit. The design equations are below.

Second Order APF Design Equations

To design a second order All Pass filter:

Choose a value for C and determine other components as per the following equations:

• k = 2 * π * Fo * C
• R2 = (2 * Q) / k
• R1 = 1 / (2 * k * Q)
• R3 = R1
• R4 = Q² * R3

Note: These filters haven’t been realized by anyone at RF Wireless World.