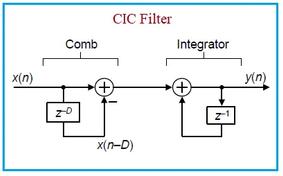
Block vs. Convolutional Interleaver: A Detailed Comparison
Advertisement
This article compares Block Interleavers and Convolutional Interleavers, highlighting their differences and applications in digital communication systems.
Introduction:
In wireless systems, a transmitted signal passes through a channel that can introduce impairments. A channel with memory exhibits mutually dependent signal transmission impairments. A prime example is a channel experiencing multipath fading. This can lead to burst errors caused by channel distortions, fading, lightning, or switching events.
To combat burst errors in memory channels, rearranging the symbols can spread them out over time. Interleaving techniques achieve this separation, effectively transforming the channel with memory into a memoryless channel, enabling the system to handle random, independent errors.
What is Interleaving?
Interleaving separates codeword symbols in time, transforming a channel with memory into a memoryless one. This allows the use of random error correcting codes in a burst noise channel. Interleaving is applied to the coded message before transmission, with deinterleaving performed after reception. The burst of errors is spread out in time, allowing the decoder to handle them effectively.

An interleaver that shuffles code symbols over several block lengths is known as a block interleaver, while one that shuffles over several constraint lengths is a convolutional interleaver. The required span is determined by the burst duration. The figure above depicts codewords without and with interleaving.
Three main types of interleavers are used in communications: Block, Convolutional, and Pseudorandom.
Block Interleaver
A block interleaver accepts coded symbols in blocks from the encoder, shuffles them, and feeds the rearranged symbols to the data modulator. This shuffling is accomplished by filling the columns of an M-row by N-column (M x N) array with the encoded sequence. After the array is filled, these symbols are fed to the modulator one row at a time and transmitted over the channel. At the receiver, the deinterleaver performs the inverse operation: symbols are entered by rows and removed one column at a time.

Example: As shown in the figure above, 24 code symbols are placed into the interleaver input. The output sequence to the transmitter consists of code symbols removed from the array row by row.
Block interleavers are further categorized into subtypes such as Matrix Interleavers, Helical Interleavers, Random Interleavers, and Odd-Even Interleavers.
Convolutional Interleaver
- Code symbols are sequentially shifted into a bank of “N” registers.
- Each successive register provides “J” symbols more storage than the preceding one.
- The zeroth register provides no storage.
- A new code symbol is shifted in while the oldest symbol is shifted out to the modulator or transmitter.

The performance of a convolutional interleaver is similar to that of a block interleaver.
Block Interleaver vs. Convolutional Interleaver: Delay and Memory Comparison
The following table highlights the differences between block interleavers and convolutional interleavers in terms of delay and memory size. Convolutional interleavers offer a reduction of one-half in both delay and memory.
| Parameters | Block Interleaver | Convolutional Interleaver |
|---|---|---|
| Delay | 2MxN-2M+2 | M(N-1) /2 |
| Memory | M x N (In Theory), 2M x N (In Practice) | M (N-1) / 2 (In theory) |
Also, refer to the benefits or advantages of interleaving in data communication.
MATLAB Code of Interleaver and Deinterleaver
The following is the MATLAB code for interleaving equations, as per IEEE 802.16 WiMAX OFDM physical layer specifications.
% Interleaver PART
s=ceil(ncpc/2);
k=0:ncbps-1;
%First permutation of interleaver
m=(ncbps/12)*mod(k,12)+floor(k/12);
%Second permutation of interleaver
n=s*floor(m/s)+mod(m+ncbps-floor(12*m/ncbps),s);
interleaved_data_out(n+1)=interleaver_input(k+1) % OUTPUT of interleaver
Advertisement
 RF
RF