Terminology » RF Basics » Kirchhoff's Current Law (KCL) vs. Kirchhoff's Voltage Law (KVL)

Kirchhoff's Current Law (KCL) vs. Kirchhoff's Voltage Law (KVL)

circuit kirchhoff current voltage kcl kvl

This article outlines the basic differences between Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL). These are two fundamental laws in circuit analysis. KCL deals with current flow, while KVL deals with voltage drops within a closed network.

Kirchhoff’s Current Law (KCL)

Kirchhoff current law-KCL

KCL states that “the algebraic sum of currents at any node of a circuit is zero.”

⇒ i1 + i2 - i3 - i4 - i5 = 0

In simpler terms, the sum of currents entering a node must equal the sum of currents leaving that node.

⇒ i1 + i2 = i3 + i4 + i5

Example:

Given i1 = 10, i2 = 6, and i5 = 4, find the other currents (i3, i6, i7).

  • By observation and using KCL, i1 = i7, therefore i7 = 10.
  • At node A, applying KCL: i1 = i2 + i4 ⇒ 10 = 6 + i4 ⇒ i4 = 4
  • At node B, applying KCL: i2 = i3 + i5 ⇒ i3 = i2 - i5 = 6 - 4 = 2
  • At node C, applying KCL: i7 = i5 + i6 ⇒ i6 = i7 - i5 = 10 - 4 = 6

Kirchhoff’s Voltage Law (KVL)

Kirchhoff voltage law-KVL

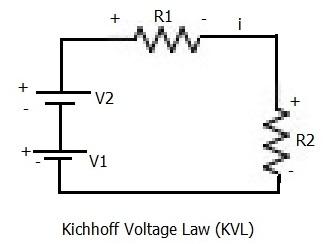
KVL states that “the algebraic sum of voltages (or voltage drops) in any closed path of a network, when traversed in a single direction, is zero.”

As per the network depicted in Figure 2 and applying KVL in a counter-clockwise direction:

⇒ -V1 + (-V2) + i*R1 + i*R2 = 0