Butterworth vs. Chebyshev vs. Bessel vs. Elliptic Filters

This page compares Butterworth, Chebyshev, Bessel, and Elliptic filters, highlighting the basic differences between them. As we know, a filter is a module that passes certain frequencies and stops others, according to its design.

There are two main categories of filters: analog and digital. Analog filters operate on analog input frequencies, while digital filters operate on digital input data.

Within each category, there are various types of filters, such as Low Pass Filter (LPF), High Pass Filter (HPF), Band Pass Filter (BPF), and Band Stop Filter (BSF). These names are based on their operational functionalities. For example, an LPF passes all frequencies in the lower band and stops frequencies in the higher band. These considerations are made with reference to a specific cutoff frequency during the design process.

Based on technical design specifications, there are also filter types such as Butterworth, Chebyshev, Bessel, and Elliptic filters. Each has its own unique characteristics, making them suitable for different applications.

The following sections describe the differences between these filter types.

Butterworth Filter

The major unique characteristics of the Butterworth filter are:

• Maximally flat response within the passband of the filter.
• Moderate phase distortion.

A Butterworth LPF will have all its poles located on the unit circle with equal angular spacing.

Chebyshev Filter

As the name suggests, the Chebyshev filter allows ripples in the passband amplitude response. It’s also known as an equal ripple response filter. The amount of ripple is a design parameter for this type of filter.

This filter type has a steeper roll-off near the cutoff frequency compared to the Butterworth filter. However, this results in non-monotonicity in the passband region along with a poorer transient response.

Key characteristics of the Chebyshev filter:

• Ripple in the passband.
• Sharper transition band compared to Butterworth.
• Poorer group delay.

The poles of this filter are located on an ellipse inside the unit circle.

Bessel Filter

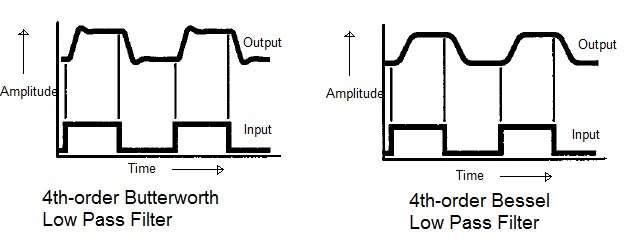
As shown in the figure, applying a non-sinusoidal waveform (such as a square wave) as input to a Butterworth low pass filter can result in distortion. The resulting output waveform may exhibit ringing and overshoot. This is because the component frequencies of the square wave shift in time relative to each other.

This happens because if the phase increases linearly with frequency, it will result in a delay in the output signal by a constant time period.

The Bessel filter avoids this situation. It introduces a linear phase shift with respect to frequency, acting as a delay line with low pass characteristics. With this type of filter, the output waveform will not have ringing or overshoot, as depicted in the figure. It will round off the input square wave at points where high-frequency harmonic components are present in the input waveform.

Elliptic Filter

• This type of filter has a sharper cutoff slope compared to Butterworth, Chebyshev, and Bessel filters.
• However, it will have ripples in both the passband and stopband of the amplitude response.
• It exhibits a very non-linear phase response.