Implementing a Low-Pass FIR Filter in Python

This article details how to implement a low-pass filter in Python, including the code and resulting plots. This specific implementation showcases a Butterworth-type low-pass filter.

Introduction

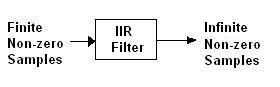
FIR (Finite Impulse Response) filters use only current and past input samples to calculate the current output sample value. Critically, they do not use past output samples.

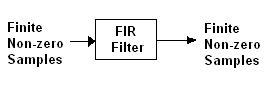Figure: FIR filter

A simple FIR equation is shown below:

$y(n) = h(0)x(n) + h(1)x(n-1) + h(2)x(n-2) + h(3)x(n-3) + h(4)x(n-4)$

For more information, refer to the differences between FIR and IIR filters (links to an external resource comparing FIR vs IIR filters are recommended here).

FIR Filter Python Code

Here’s the Python code for implementing an FIR filter using the scipy.signal library:

import matplotlib.pyplot as plt
import scipy.signal as sig
import numpy as np
from math import pi

plt.close('all')

# Filter parameters
N = 20        # Filter order
fc = 100      # Cutoff frequency (Hz)
Fs = 1000     # Sampling frequency (Hz)
w_c = 2 * fc / Fs  # Normalized cutoff frequency

# Design the FIR filter using a window method (e.g., Hamming window)
t = sig.firwin(N, w_c)

# Calculate the frequency response of the filter
[w, h] = sig.freqz(t, worN=2000)
w = Fs * w / (2 * pi)  # Convert normalized frequency to Hz
h_db = 20 * np.log10(abs(h)) # Convert magnitude to dB

# Plot the frequency response
plt.figure()
plt.plot(w, h_db)
plt.title('FIR filter response')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude (dB)')
plt.show()

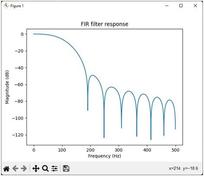
FIR Python Output Plots

The following plots are generated by the above Python code:

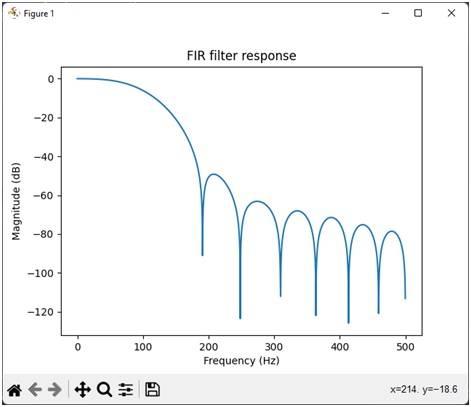Figure: FIR filter python output plots