What is RF Filter ?

An RF (Radio Frequency) filter is an electronic component used in wireless communication systems to pass desired range of frequencies and blocks undesired range of frequencies. RF filters play a crucial role in radio transmitters and receivers to ensure efficient signal transmission and reception respectively. There are several types of RF filters such as Low Pass Filter, High Pass Filter, Band Pass Filter and Band Stop Filter based on their distinct characteristics. RF filter design requires a deep understanding of RF concepts, circuit design and practical implementation considerations as per desired filter type and its specifications.

The diagram is of RF up converter which converts IF frequency to RF frequency using heterodyne approach using two RF mixers. It is transmitter part of C band RF transceiver used in VSAT. IF input frequency range is from 52 to 88 MHz and RF frequency output is from 5925 to 6425 MHz. In this RF up converter design, there are three RF filters viz. low pass filter (LPF) at input, band pass filter (BPF) after first mixer and one more BPF after second mixer.

At the input 52-88 MHz low pass filter is used using discrete components. This signal beats with 1112.5 MHz signal gives 1182.5 MHz signal output and other products from the mixer. After first mixer BPF (band pass filter) which passes 1182.5 MHz with bandwidth of 36MHz is employed. Later after second stage of mixing, 5925 to 6425 MHz microstrip based parallel coupled band pass filter is incorporated.

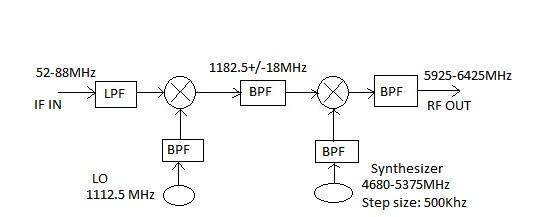
In the first stage of mixing, local oscillator of fixed value 1112.5MHz is passed through microstrip based 3-4 stage hairpin RF filter can be used. The round corner edge coupled band pass filter of microstrip type is used to filter the output of synthesizer of value 4680 to 5375MHz.

RF Low Pass Filter design example

Let us take example of rf low pass filter design using following specifications:
Impedance: 50 Ohm
Cutoff frequency (Fc): 3 GHz
Equi-ripple: 0.5dB
Rejection: 40 dB at 2*Fc

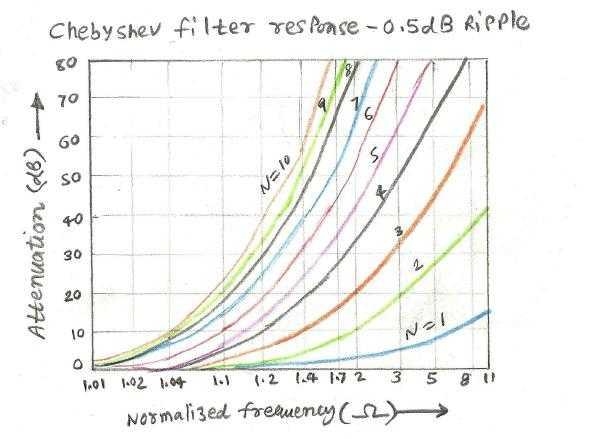
Step 1: First determine normalized frequency, which in this case is w/wc, equals to 2 (6GHz/3GHz). Determine filter type based on ripple required, which in this case is about 0.5dB, hence chebyshev topology of filter will be ideal choice. There are various filter topologies such as Butterworth, Chebyshev, Bessel or Elliptic. Appropriate topology is chosen based on the filter type and design specifications.

Now based on normalized frequency (2) and attenuation (40dB) and using the filter response curve (chebysev LPF with 0.5 dB ripple), determine filter order (N) required for the design. Filter response will have normalized frequency on X axis and Attenuation on Y axis. Different filter orders are plotted against these two. Doing so from 40dB and normalized frequency of 2 we get filter order of value 5 from the curve for our rf filter design.

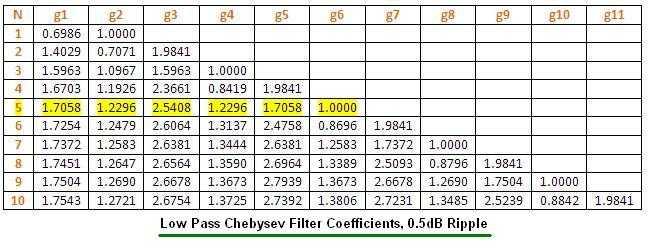
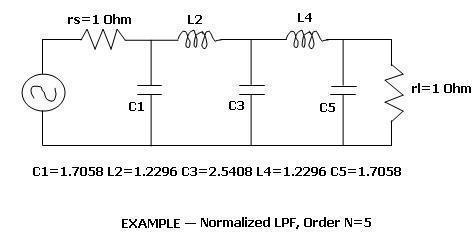
Based on filter order N (here 5) and using Filter coefficients table as mentioned above for Chebysev LPF for 0.5dB ripple we will determine filter coefficients, which are g1=1.7058,g2=1.2296,g3=2.5408,g4=1.2296,g5=1.7058,g6=1. The figure above mentions low Pass Chebysev Filter Coefficients for 0.5dB ripple for various orders of the filter. Following figure mentions LPF with order N using discrete L and C components.

Step 2: Now use Richard transformation to replace inductor by short circuit line and capacitor by open circuit line. Length of the lines should be λ/8. Figure 4 below is obtained after Richard- transformation is applied to discrete circuit in figure 4 for rf filter design.

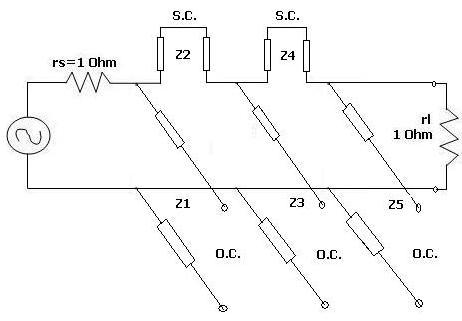
Step 3: Now convert all the short circuited stubs, which are in series into shunt connected open circuit stubs. This can be achieved using Kudora's identities. This is depicted in figures 6-9 below. To apply Kudora's identity unit elements are introduced in the circuit where ever required as shown in figures below.

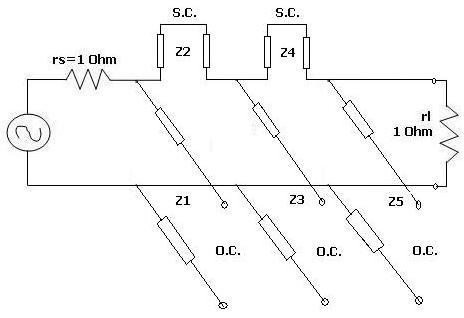
In figure 6, unit element is inserted at the input and output without changing rest of the elements. Now Z1 and Z5 are converted from open circuit shunt elements to the short circuit series elements.

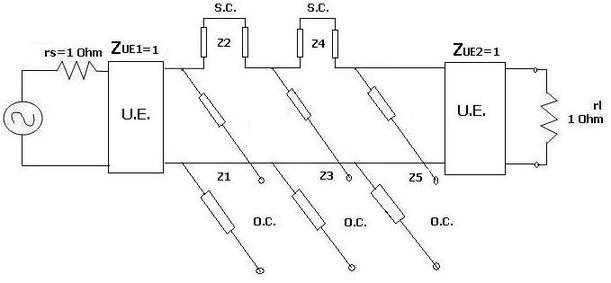
Now two more unit elements are inserted at the source and destination. And using Kudora's identities z1,z2,z4 and z5 elements are converted from S.C. series elements to the O.C. shunt elements

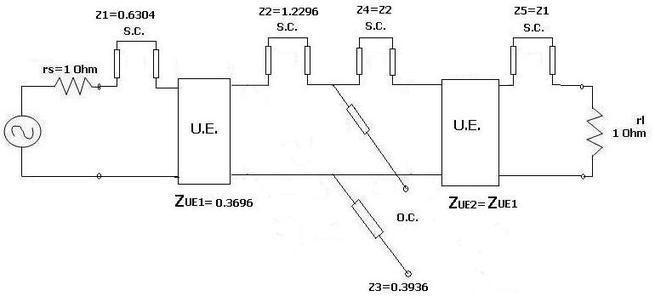
The same RF filter design is incorporated using built in micro strip line elements in RF/microwave design software such as Agilent EESoF or ADS or microwave office from AWR.

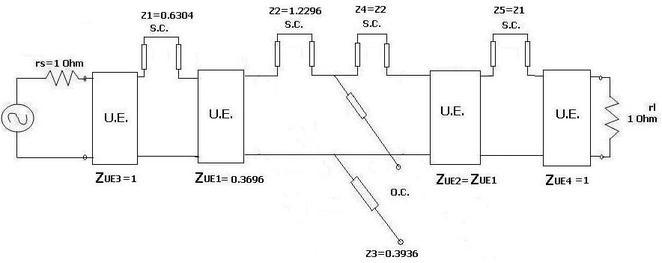
Step 4: Following is the realization of RF filter as micro-strip based on specifications mentioned at the beginning of this article.

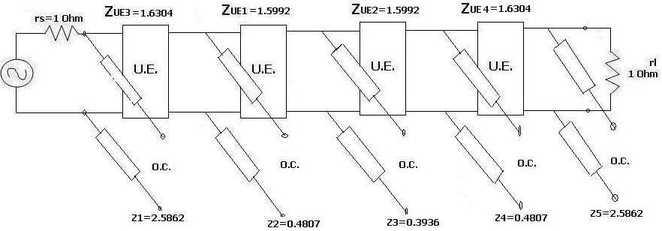
Step 5: This microstrip layout mentioned in figure.10 is etched on the respective dielectric based on frequency of operation as mentioned and tested with connectors using scalar network analyzer (SNA).

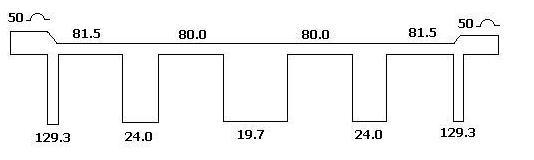
Conclusion

The same design approach or method can be applied to rf bandpass filter design and other types. It has to be noted that select filter order "N" as per normalized frequency versus attenuation curve. Based on this filter order "N", appropriate filter coefficients have to be extracted from the table as per desired ripple.

RF Filter Related Links

RF RELATED LINKS

RF and Wireless Terminologies